图神经网络概述

摘要

传统深度学习的数据——欧氏空间中的数据; 与之相对——图数据, 对象之间关联和依赖复杂. 本文对基于图数据的深度学习——图神经网络 (GNN)做一综述，并给出一种新的GNN的分类方法：循环GNN (recurrent GNN)，卷积GNN (convolutional GNN)，图自编码器 (graph autoencoder)，时空GNN (spatial–temporal GNN). 进一步讨论GNN在不同领域的应用, 总结开源代码, 测试数据集及模型评估. 最后提出有潜力的研究方向.

介绍

实时目标检测[1][2], 机器翻译[3][4], 语音识别[5]这些曾经依赖手工提取格式化特征的数据集的机器学习任务, 利用端到端的深度网络已经取得了革命性的进展, 如CNN[6], RNN[7], 自编码器[8]. CNN能够探索图片数据的特性如平移不变性(shiftinvariance), 局部连通性(local connectivity), 及复合性(compositionality)[9].

使用图数据的场合: 电子商务, 化学 (如分子结构, 生物活性领域), 文献引用网络. 图可以非常不规则: 可变数量的无序的结点, 各结点不同数量的相邻结点. 导致图像领域的操作 (如卷积等) 在图领域非常困难. 进一步, 现有机器学习算法一个核心的假设: 样本间相互独立亦不满足.
近期, 传统深度学习的定义和技术被推广到了图上. 例: 图的卷积, 图像可视作特殊的图, 其每个像素与临近像素相连.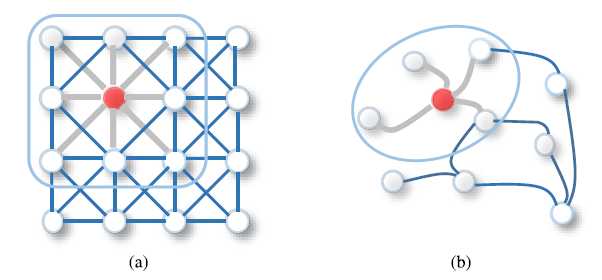

在(a)中, 隐藏层中红色的点的值由输入层对应的9个点计算卷积得出, 权重由卷积核决定. 在(b)中, 亦取结点及相邻结点加权得到. 注意邻近结点无序, 且数量不固定.

[9]是第一篇GNN的review, 主要关注GCN; [10]关注网络嵌入问题; [11]将图网络视作学习关联性数据的基石, [12]在图神经网络中引入了注意力机制(attention mechanism).

本文的工作:

1. 新的分类方法 (四类):
   循环GNN (recurrent GNN, RecGNN), 卷积GNN (convolutional GNN, ConvGNN), 图自编码器 (graph autoencoder，GAE), 时空GNN (spatial-temporal GNN, STGNN).
2. 详细的综述: 包括模型介绍, 比较, 算法总结等
3. 丰富的资源: 最先进的模型, 测试数据集, 开源代码, 实践应用.
4. 未来研究方向 (四类):
   模型的深度 (depth), 扩展性 (scalability), 齐次性 (heterogenity), 动态性 (dynamicity).

GNN背景及定义

背景

GNN简史

[13]首次将神经网络引入有向无环图. 早期研究集中于 RecRNN, 他们通过迭代地传播一个节点周围的信息, 直到形成一个稳定的不动点, 来学习该结点的表示 (representation). 缺点是计算花销大, [17][18]做了改进.

受CV领域CNN的启发, 兴起了大量对ConvGNN的研究, 主要可分为两个流派: 基于谱的方法 (spectral-based approaches) 和基于空间的方法 (spatial-based approaches). 前者第一个著名的研究是[19], 基于谱图理论研究了图的卷积, 之后[20][21][22][23]做了提升和拓展. 基于空间的ConvGNN 的研究要更早: [24]通过复合非回归层同时利用RecGNN中信息传递的观点解决了图的相互依赖问题.(这是什么? …) 基于空间的ConvGNN的研究进一步有[25][26][27]. 除RecGNN, ConvGNN外, 还出现了其他GNN的变种, 如GAE, STGNN等, 他们的框架可以建立在RecGNN, ConvGNN之上.

GNN v.s. 网络嵌入

GNN与图 (或网络) 嵌入关系密切, 后者相关研究有[10][28][29][30][31][32]. 网络嵌入的目的是将网络表示为低维向量, 并保留网络的拓扑结构和结点的内容信息. 以便于之后的图分析 (例如分类, 聚类, 推荐) 可以使用现成的机器学习算法进行. 许多网络嵌入算法是典型的无监督算法, 可以粗略地分为三类: 矩阵分解[33][34], 随机游走[35], 和深度学习方法. 网络嵌入的深度学习同时属于GNN, 包括图基于自编码器的算法 (例如DNGR[59]和SDNE[60]) 和无监督训练下的图卷积网络(如GraphSAGE[42]). 下图表示了网络嵌入和GNN的关系:

GNN v.s. 网络嵌入

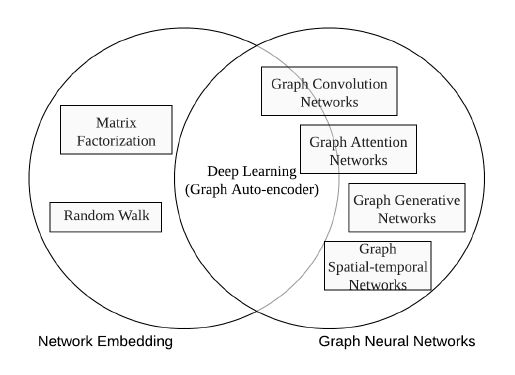
GNN v.s. 图核方法 (Graph Kernel Methods):

图核是历史上著名的用来解决图分类问题的技术[36][37][38], 这些方法采用核函数来度量一对图之间的相似度, 目的是使基于核的算法 (如支持向量机) 可以被用于图的监督学习. 与GNN (基于深度学习的?) 类似, 图核将图或结点通过映射函数嵌入向量空间. 区别在于映射函数是确定的而不是学习到的. 由于要逐对计算相似度, 所以图核方法面对的计算瓶颈非常明显. 与之相对, GNN直接基于提取出的图表示 (graph representation) 进行图分类, 因此比起图核方法更加高效. 关于图核方法的进一步回顾见[39].

定义

1. 图 (Graph)
   图: $G=(V, E)$, 其中$V$是结点集合, $E$是边集合. 图的结点记作$v_i\in V$, 边记作$e_{ij}=(v_i, v_j)\in E$. 结点$v$的”邻居”记作$N(v)=\{u\in V|(u,v)\in E\}$. 邻接矩阵记作$\mathbf{A}\in \mathbb{R}^{n\times n}$, 其中$\mathbf{A}_{ij}=1$, 若$e_{ij}\in E$; $\mathbf{A}_{ij}=0$, 若$e_{ij}\notin E$. 一个图可以带有结点属性(node attribute) $\mathbf{X}$, 称为属性图 (attributed graph), 其中$\mathbf{X}\in \mathbb{R}^{n\times d}$是结点特征矩阵, 其行向量$\mathbf{x}_v\in \mathbb{R}^d$是结点$v$的特征向量. 同时, 一个图可以带有边属性$\mathbf{X}^e$, 其中$\mathbf{X}^e\in \mathbb{R}^{m\times c}$是边特征矩阵, 其行向量$\mathbf{x}^e_{v,u}\in \mathbb{R}^c$表示边$(v, u)$的特征向量.
2. 有向图 (Directed Graph)
   一个图是有向的, 当且仅当其每一边都有向地从一个结点指向另一个结点. 无向图是特殊的有向图, 若无向图的两结点相连, 则存在一对反向的边连接这两点. 一个图是无向的当且仅当其邻接矩阵对称.
3. 时空图 (Spatial–Temporal Graph)
   一个图称为时空图, 若其节点属性随时间动态变化. 记为$G ^ { ( t ) } = \left( \mathbf { V } , \mathbf { E } , \mathbf { X } ^ { ( t ) } \right)$
4. 其他记号见下表 表1 常用记号

分类及架构

分为四类: 循环GNN (recurrent GNN, RecGNN), 卷积GNN (convolutional GNN, ConvGNN), 图自编码器 (graph autoencoder，GAE), 时空GNN (spatial-temporal GNN, STGNN), 以下首先对各类做一简介:

GNN的分类

1. 循环GNN
   这些大多数是GNN开创性的工作. 循环GNN的目的是通过循环神经架构 (recurrent neural architecture) 学习结点的表示. 它假设图中的一个结点始终与其相邻结点交换信息, 直到形成一个稳定的平衡. 观念上, RecGNN很重要, 相关研究启示了ConvGNN的研究, 特别地, 基于空间的ConvGNN继承了其信息传递的观点.
2. 卷积图神经网络
   它将卷积操作从网格数据推广到图数据, 主要观点是结点$v$利用其自身的特征$\mathbf { x } _ { v }$及其相邻节点的特征$\mathbf { x } _ { u }, u\in N(v)$聚合生成结点$v$的表示. 与RecGNN不同, ConvGNN将多个图卷积层堆 (stack) 起来, 以提取更高水平的结点表示. ConvGNN对构建其他复杂的GNN起着核心的作用.图(a): 用ConvGNN进行结点分类. 图(b): 用ConvGNN进行图分类.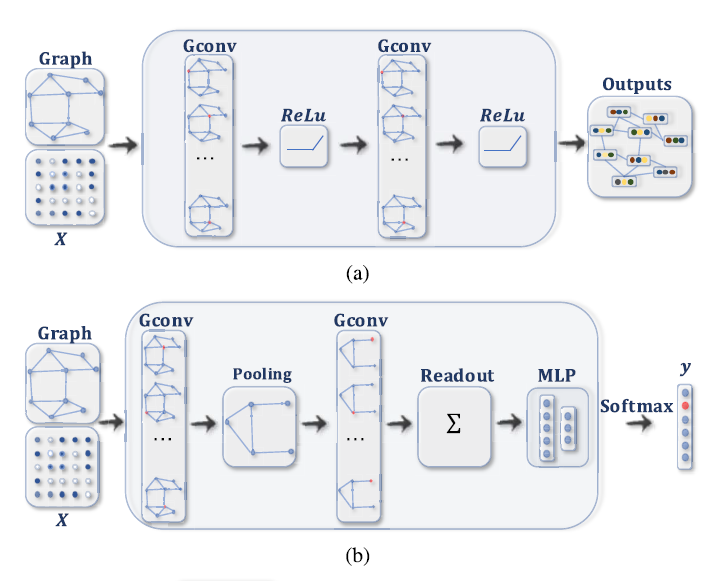 (a) 多层卷积层的ConvGNN. 一个卷积层包含每个结点的隐藏表示 (为其相邻节点的特征信息的聚合), 聚合后通过一个非线性函数. 通过多个隐藏层叠加, 每个结点最后的隐藏表示可以接受到来自更远结点的信息. (b)带有池化层和readout层的ConvGNN, 用于图分类. [21]一个图卷积层后接一个池化层用于将图粗化为一个子图, 以便得到水平更高 (higher graph-level) 的结点表示. 一个 readout 层将图最终表示为子图的隐表示.
3. 图自编码器
   这是一种将结点/图通过编码嵌入潜在的向量空间, 以及从编码信息中重建图的无监督学习框架. GAE用来学习网络嵌入和图的生成分布. 对网络嵌入, GAE通过重建图结构信息 (如邻接矩阵) 学习潜在结点表示. 一些方法分步生成图, 另一些方法一次性生成图. (c)展示了GAE如何用于网络嵌入.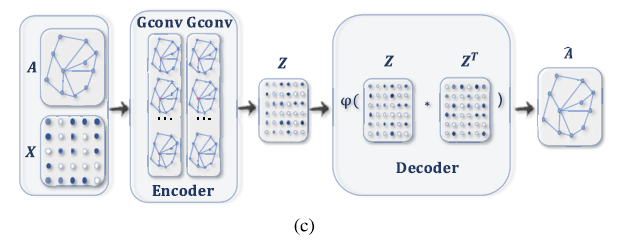 GAE用于图嵌入[61]. 编码器使用图卷积层得到每个结点的一个网络嵌入. 给定网络嵌入后, 解码器逐对计算距离. 在施以非线性激活函数之后, 解码器可以重建邻接矩阵. 通过最小化实际邻接矩阵和恢复得到的邻接矩阵来训练网络.
4. 时空GNN
   目的是从时空图中学习隐藏的模式, 在交通速度预测, 驾驶员操作预估以及人的动作识别等邻域作用越来越重要. 目前许多方法加入图卷积以获取空间依赖关系, 同时利用RNN或CNN来建模时间上的依赖关系. (d)展示了用时空图进行预测.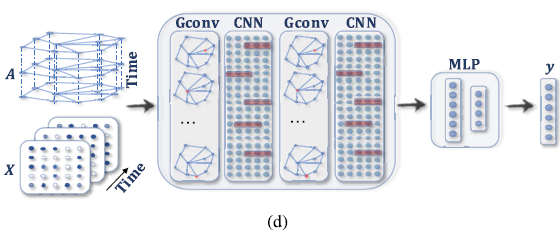 STGNN用于时空图的预测[74]. 一层图卷积层之后接一层一维CNN. 图卷积层在$A$和$\mathbf{X}^{(t)}$上操作, 以捕获空间依赖; 一维CNN在X上沿时间轴滑动以捕获时间依赖. 输出层是一个线性变换, 生成对每个结点的预测, 如下一个时间上的预测值.

下表做了一个详细的分类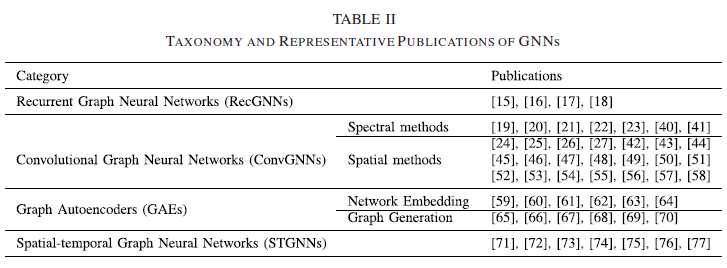

架构

有了图结构和结点信息作为输入, GNN的输出可以关注带有如下机制的图分析任务.

1. 结点层面: 输出与结点回归或结点分类相关. RecGNN和ConvGNN可以通过信息传播和图卷积提取高级的结点表示. 利用一个多层感知机或softmax层, GNN能够以端到端的方式处理结点层面的任务.
2. 边层面: 与边分类和连接预测相关的任务.
3. 图层面: 图分类任务. 池化和readout.

训练架构
半监督或纯非监督学习, 端到端学习架构, 取决于学习任务及标签信息.

1. 半监督学习用于结点分类
   部分结点有标签, GNN可以学习识别无标签结点的标签[22]. 用卷积层和softmax层.
2. 监督学习用于图分类
   用于预测整个图的标签[52][54][78][79]. 卷积层+池化层+readout层.
3. 非监督学习用于图嵌入
   图中没有标签时用非监督学习. 可以通过两种方式求得边层面的信息: 一种是利用自编码器的架构, 编码器嵌入隐向量空间, 解码器重构. [61][62]. 另一种是利用负采样[42].

表III总结了RecGNN和ConvGNN的主要特征, 并比较了输入材料, 池化层, readout层及时间复杂度. 更详细地, 比较了信息传递/图卷积的时间复杂度. [19][20]需要特征分解, 时间复杂度为$\mathcal{O}\left(n^3\right)$. [46]计算了每对结点间的最短路径, 因此时间复杂度也是$\mathcal{O}\left(n^3\right)$. 其他方法在邻接矩阵稀疏的时候时间复杂度是$\mathcal{O}\left(m\right)$, 否则则是$\mathcal{O}(n^2)$. 这是因为在这些方法中计算每个结点$v_i$的表示涉及它的$d_i$个相邻节点, 对$d_i$求和就是边的数量. 表III中部分方法缺失时间复杂度.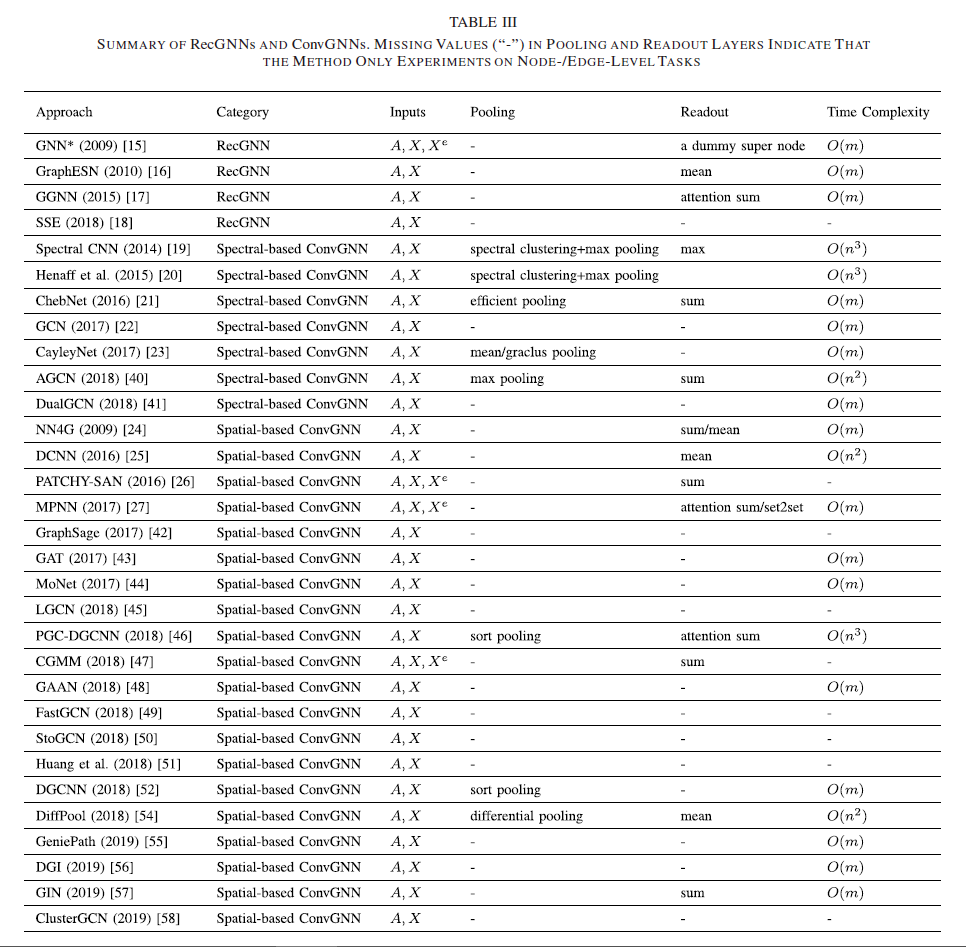

循环图神经网络

RecGNN实现了参数共享, 受限于算力, 早期研究集中于有向无环图[13][80].

GNN*将以前的循环模型推广到一般类型的图上, 如无环, 有环, 有向, 无向图. GNN*按如下方式更新结点的隐向量:

$$\mathbf { h } _ { v } ^ { ( t ) } = \sum _ { u \in N ( v ) } f \left( \mathbf { x } _ { v } , \mathbf { x } _ { ( v , u ) } ^ { \mathrm { e } } , \mathbf { x } _ { u } , \quad \mathbf { h } _ { u } ^ { ( t - 1 ) } \right)$$

其中$f(\cdot)$是参数化的函数, 为确保收敛要求$f$是紧映射. $\mathbf { h } _ { v } ^ { ( 0 ) }$随机初始化. 若$f$是神经网络, 需要对Jacobian矩阵施以惩罚项. 当收敛准则满足时, 最后一步传给readout层. GNN*改变了结点状态传递的阶段和参数梯度计算的阶段来最小化目标函数, 这一策略使得GNN*能够处理有环图. 此后, GraphESN[16]将echo state network推广到图上以提升训练效率. GraphESN包含一个编码器和一个输出层, 编码器随机初始化, 不需要训练, 同时使用收缩状态转移函数以循环更新节点状态. 输出层以固定的结点的状态作为输入.

GGNN[17]引入了门控循环单元 (GRU)[81]作为循环函数, 将循环限制为固定次数. 优点在于不需要限制参数来保证收敛. 结点的隐状态由结点之前的隐状态及其相邻节点的隐状态更新:

$$\mathbf { h } _ { v } ^ { ( t ) } = \operatorname { GRU } \left( \mathbf { h } _ { v } ^ { ( t - 1 ) } , \sum _ { u \in N ( v ) } \mathbf { W h } _ { u } ^ { ( t - 1 ) } \right)$$

其中$\mathbf { h } _ { v } ^ { ( 0 ) } = \mathbf { x } _ { v }$. 与GNN*和GraphESN不同, GGNN使用BPTT (backpropagation through time) 算法训练模型参数. 这会导致一个问题, 对于较大的图, GGNN需要在所有结点上多次运行循环函数, 这要求将所有结点的中间状态存储在内存中.

随机稳定状态嵌入 (Stochastic steady-state embedding, SSE)提出了一种更易扩展到大型图上的算法[18]. SSE采用一种随机且非同时的方式更新. 它选出一批结点用于状态更新, 另一批节点用于梯度计算. 节点更新时为了保持稳定, 采取了之前状态和现在状态的加权和:

$$\mathbf { h } _ { v } ^ { ( t ) } = ( 1 - \alpha ) \mathbf { h } _ { v } ^ { ( t - 1 ) } + \alpha \mathbf { W } _ { 1 } \sigma \left( \mathbf { W } _ { 2 } \left[ \mathbf { x } _ { v } , \sum _ { u \in N ( v ) } \left[ \mathbf { h } _ { u } ^ { ( t - 1 ) } , \mathbf { x } _ { u } \right] \right] \right)$$

SSE没有从理论上证明结点状态会逐步收敛到不动点.

卷积图神经网络

ConvGNN不是在收缩限制下迭代地更新结点状态. ConvGNN在架构上使用数量固定的层 (层中的权重不同) 以解决环的相互依赖 (?). 其最大的区别见下图: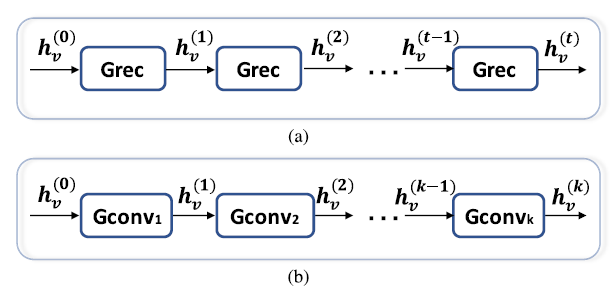

(a)RecGNN使用相同的图循环层Grec更新结点表示, (b)ConvGNN使用不同的图卷积层Gconv.
ConvGNN分为两类: 基于谱和基于空间. 基于谱的方法通过引入图像信号处理[82]中的滤波器 (filter) 来定义图卷积. 基于空间的方法继承了来自RecGNN的方法, 通过信息传播定义图卷积. 自从GCN[22]弥合了基于谱的方法和基于空间的方法之间的gap以来, 谱方法以其高效, 灵活和普适的特性迅速发展.

基于谱的ConvGNN

背景: 图像信号处理[82][83][84]. 假设图无向, 规范化的图拉普拉斯矩阵定义为

$$\mathbf { L } = \mathbf { I } _ { \mathbf { n } } - \mathbf { D } ^ { - ( 1 / 2 ) } \mathbf { A D } ^ { - ( 1 / 2 ) },$$

其中$\mathbf { D }$是结点度的对角矩阵, 定义为$\mathbf { D } _ { i i } = \sum _ { j } \left( \mathbf { A } _ { i j } \right).$ 该矩阵保留了实对称半正定的性质, 从而有分解:

$$\mathbf { L } =\mathbf { U } \mathbf { \Lambda } \mathbf { U } ^ {\top},$$

其中$\mathbf { U } = \left[ \mathbf { u } _ { \mathbf { 0 } } , \mathbf { u } _ { 1 } , \ldots , \mathbf { u } _ { \mathbf { n } - 1 } \right] \in \mathbb { R } ^ { n \times n }$是特征向量矩阵, $\mathbf { \Lambda }$是特征值 (谱) 构成的对角矩阵, $\mathbf { \Lambda }_{ii}=\lambda_i$. $\mathbf{L}$的特征向量生成一个正交空间: $\mathbf { U } ^ { \top } \mathbf { U } = \mathbf { I }$. 在图信号处理中, 一个图信号$\mathbf { x } \in \mathbb { R } ^ { n }$是一个图的所有结点的特征向量 (feature vector), 其中$x_i$是第i个结点的值. 对信号$\mathbf { x }$的图傅立叶变换定义为

$$\mathscr { F } ( \mathbf { x } ) =\mathbf { U } ^ { \top } \mathbf { x },$$

逆图傅立叶变换定义为

$$\mathscr { F } ^ { - 1 } ( \hat { \mathbf { x } } ) = \mathbf { U } \hat { \mathbf { x } },$$

其中$\hat { \mathbf { x } }$是图傅立叶变换的结果信号. 图傅立叶变换将输入的图信号映到正交空间, 其基由$\mathbf{L}$的特征向量组成. 变换后的信号$\hat { \mathbf { X } }$的元素是图信号在新的空间里的坐标. (事实上: $\mathbf{x}=\mathbf{U}\hat{\mathbf{x}}=\sum_{i=0}^{n-1}\hat{x}_i\mathbf{u}_i$, 即向量$\hat{\mathbf{x}}$是$\mathbf{x}$用$\{\mathbf{u}_i\}_{i=0}^{n-1}$这组基向量线性表示的系数.) 现在, 输入信号$\mathbf{x}$关于滤波器$\mathbf { g } \in \mathbf { R } ^ { n }$的卷积定义为:

$$\begin{aligned} \mathbf { x } * _ { G } \mathbf { g } &= \mathscr { F } ^ { - 1 } ( \mathscr { F } ( \mathbf { x } ) \odot \mathscr { F } ( \mathbf { g } ) )\\ &= \mathbf { U } \left( \mathbf { U } ^ { T } \mathbf { x } \odot \mathbf { U } ^ { T } \mathbf { g } \right) \end{aligned}$$

其中$\odot$是哈达玛积. 若记滤波器为$\mathbf { g } _ { \theta } = \operatorname { diag } \left( \mathbf { U } ^ { T } \mathbf { g } \right)$, 则谱图卷积可以简化为:

$$\mathbf { x } * _ { G } \mathbf { g } _ { \theta } = \mathbf { U } \mathbf { g } _ { \theta } \mathbf { U } ^ { T } \mathbf { x }.$$

所有基于谱的卷积区别仅在于滤波器的选取.