前深度学习时代（一）

矩阵分解算法——协同过滤的进化

协同过滤的问题

1. 推荐结果的头部效应明显，处理稀疏向量的能力弱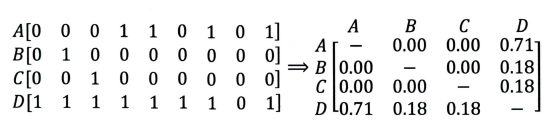： 如上图所示，横坐标（A，B，C，D）表示物品，纵坐标表示用户评价。物品A, B, C彼此间相似度为0，且均与物品D有很大的相似度，但这很可能不是由于物品本身的相似度导致的。A, B, C相似度小可能由于A, B, C为非常冷门的物品，其特征向量非常稀疏，D则反之。这揭示了协同过滤难以处理稀疏向量的问题。
2. 仅利用物品与用户的交互信息，无法引入其他物品特征及用户特征。

矩阵分解算法的原理

1. 为每一个用户和物品生成一个隐向量（比如$\mathbb{R}^2$上的一个二位坐标向量），将距离用户相近的物品推给用户，这一向量通过分解共现矩阵实现： $$R_{m\times n}=U_{m\times k}V_{k\times n}$$ 其中$R$为共现矩阵，$U$为用户矩阵，$V$为物品矩阵；$m$为用户数量，$n$为物品数量，$k$是隐向量的维度。$k$决定了隐向量表达能力的强弱：$k$越大，泛化程度越低，越容易过拟合；反之相反。
2. 基于用户矩阵$U$和物品矩阵$V$，可以预估用户u对物品i的评分： $$\hat{r}_{ui}=p_u^{\top}q_i$$

矩阵分解的求解过程

主要包括三种分解方式：特征值分解，奇异值分解，梯度下降。

1. 特征值分解
   只能用于方阵，不适用。
2. 奇异值分解（SVD），核心是保留前k个奇异值： $$R=U\Sigma V^{\top},$$ 其中$U$，$V$分别为正交矩阵，$\Sigma_{m\times n} = \rm diag\{\sigma_1,\sigma_2, \cdots,\sigma_\ell, 0, \cdots, 0\}$，$\sigma_1\geqslant\sigma_2\geqslant\cdots\geqslant\sigma_\ell>0$。取 $$\Sigma^\prime=\rm diag\{\sigma_1,\sigma_2, \cdots,\sigma_k\},\quad k\leqslant\ell,$$ $$U^\prime = U_{m\times k}\quad（表示U的前k列，下同）$$ $$V^\prime = V_{n\times k}$$ 再令 $$\tilde{U}=U^\prime\Sigma^{\prime\frac{1}{2}}$$ $$\tilde{V}=V^\prime\Sigma^{\prime\frac{1}{2}}$$ 得到$R$的一个（近似）分解： $$R\approx\tilde{U}\tilde{V}$$ 奇异值分解的弊端：
   (1). 不适合处理稀疏的共现矩阵；
   (2). SVD的时间复杂度$\mathcal{O}(mn^2)$
   所以也不适用。

3. 梯度下降
   寻找最佳的分解转化为优化问题：

   $$p^*_u,\ q^*_i=\mathop{\mathrm{arg\ min}}_{p_u,\ q_i} \sum_{(u,i)\in K}(r_{ui}-p_u^\top q_i)^2$$

   进一步，可以加入正则化项：

   $$p^*_u,\ q^*_i=\mathop{\mathrm{arg\ min}}_{p_u,\ q_i} \sum_{(u,i)\in K}(r_{ui}-p_u^\top q_i)^2+\lambda\left(\Vert p_u\Vert+\Vert q_i\Vert\right)^2$$

   共$(mk+nk)$个变量需要优化。

   对$p_u$求偏导：

   $$\begin{aligned} &\frac{\partial}{\partial p_u}\sum_{(u,i)\in K}(r_{ui}-p_u^\top q_i)^2+\lambda\left(\Vert p_u\Vert^2+\Vert q_i\Vert^2\right) \\ = &\left( \sum_i-2(r_{ui}-p_u^\top q_i)q_i\right)+2\lambda p_u \end{aligned}$$

   采用随机梯度下降（随机抽取一个用户，$m=1$），对$p_u$更新：

   $$p_u^{(t+1)}=p_u^{(t)}-\gamma\left(\lambda p_u^{(t)}-(r_{ui}-p_u^{(t)\top} q_i^{(t)})q_i^{(t)} \right)$$

   同理对$q_i$更新

   $$q_i^{(t+1)}=q_i^{(t)}-\gamma\left(\lambda q_i^{(t)}-(r_{ui}-p_u^{(t)\top} q_i^{(t)})p_u^{(t)} \right)$$

   其中$\gamma$为学习率。

   梯度下降到迭代次数超过阈值或损失低于阈值时结束。

   消除用户相物品打分的偏差（？）

   $$r_{ui}=\mu+b_i+b_u+p_u^{\top}q_i$$

   分别训练$p$，$q$，$b$，$\mu$。

   矩阵分解的有点和局限性

4. 泛化能力强；
5. 空间复杂度低，不需要储存共现矩阵$R$，只需要储存$U$和$V$；
6. 更好的扩展性，便于与其他方法结合。

逻辑回归——融合多种特征的推荐模型

逻辑回归能够综合利用用户、物品、上下文等多种不同的特征，生成较为”全面”的推荐结果。逻辑回归将推荐问题看成一个分类问题（点击率（Click Through Rate，CTR）预估问题。），通过预测正样本的概率对物品进行排序。

基于逻辑回归模型的推荐流程

1. 构造特征向量；
2. 训练模型；
3. 对不同的物品，预估点击的概率；
4. 按照点击概率排序，推荐点击概率靠前的。

逻辑回归模型的数学形式（略）

逻辑回归的优势

1. 数学上的支撑：CTR模型，因变量表示点击与否，服从两点分布；
2. 可解释性强（如权重的含义）
3. 工程化需要

逻辑回归的局限性

表达能力不强，无法进行特征交叉、特征筛选等一系列较为”高级”的操作，因此不可避免地造成信息的损失。